用空间的语言表达向量、矩阵和行列式

向量：

• 字面意思：排成一列的数字。
• 实际意思：带有方向的线段、空间内的点。

矩阵：

• 字面意思：排成矩阵的数字。
• 实际意思：空间到空间的映射。

行列式：

• 字面意思：麻烦的计算。
• 实际意思：矩阵映射所对应的“体积扩大率”。

基向量

去掉向量的坐标体系，只构建一个用有向线段表示的世界，支持加法和数量乘法，称为线性空间，也叫向量空间。

当需要使用坐标进行计算时，则可以选择一组基向量实现。

作为坐标系基准的一组向量称为基底，沿着不同基准向量走的步数叫做坐标。

可逆性、秩、特征值等与基底的选择无关。

构成基向量的条件：

1. 当前空间任何向量都可以表示为各基向量的线性组合。
2. 并且这种表示方法是唯一的。

这里是直来直往的坐标体系。弯曲的坐标体系需要通过流形方法进行分析了。

维数等于基向量的个数。

有两组基底的情况下，会出现根据一组基底对应的坐标求另一组基底对应的坐标的“坐标转换”问题。

向量内积和外积

内积：

也称为点乘。

$$ \boldsymbol{a} * \boldsymbol{b} = a_1b_1 + … + a_nb_n $$

要求一维向量a和向量b的行列数相同。

点乘的几何意义是可以用来表征或计算两个向量之间的夹角，以及在 b 向量在 a 向量方向上的投影。

外积：

也称为向量积、叉乘。

外积的运算结果是一个向量而不是一个标量。并且两个向量的叉积与这两个向量组成的坐标平面垂直。

在三维几何中，向量 a 和向量 b 的叉乘结果是一个向量，更为熟知的叫法是法向量，该向量垂直于 a 和 b 向量构成的平面。

公式有点复杂：

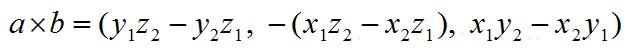
矩阵和映射

矩阵就是映射。

将 n 维向量 $\boldsymbol{x}$ 乘以 m x n 矩阵 $\boldsymbol{A}$，就能得到 m 维向量 $\boldsymbol{y} = \boldsymbol{A}\boldsymbol{x}$。也就是说，矩阵 A 确定了一个向量到另一个向量的映射。

在矩阵世界里，我们需要将列向量看作一个基本单位。映射的过程可以看作原来单位向量到当前坐标的转变。

例如，矩阵 A 是：

$$ \begin{pmatrix} 2 & 0.3 \\ 1.3 & 0.8 \end{pmatrix} $$

可以理解为第一维度 (1, 0) 点到了 (2, 1.3)，第二维度 (0, 1) 点到了 (0.3, 0.8)。

矩阵的乘积等于映射的合成。

$$ (BA)x = B(Ax) $$

先通过 A 转换，再通过 B 转换。

逆矩阵等于逆映射。

定义：对于方阵 $A$，它的逆映射对应的矩阵称为 $A$ 的逆矩阵。即，对于任意的向量 $\boldsymbol{x}$，若有 $A\boldsymbol{x}=\boldsymbol{y}$，则有 $A^{-1}\boldsymbol{y}=\boldsymbol{x}$ 成立。

逆矩阵并不一定存在。但对于任意矩阵 $A$，都有逆矩阵的推广概念——广义逆矩阵。

分块矩阵在计算时要⚠️注意它的乘法，我们可以将分块矩阵当作大矩阵的元素，运用矩阵的乘法进行操作。

矩阵既可以使用列向量表示，也可以使用行向量表示。

如果分块矩阵主对角线上的区块都是方阵，并且其他地方的矩阵都是零矩阵，则称为分块对角矩阵。 它的好处在于我们可以将整个矩阵的映射看作多个独立的变换组成，每个变换对应一个区块。