R 语言统计检验函数汇总
王诗翔 · 2019-12-25
资料来源:《R 语言核心技术手册》和 R 文档
数据基本来自胡编乱造 和 R 文档
本文基本囊括了常用的统计检验在 R 中的实现函数和使用方法。
连续型数据
基于正态分布的检验
均值检验
t.test(1:10, 10:20)
#>
#> Welch Two Sample t-test
#>
#> data: 1:10 and 10:20
#> t = -7, df = 19, p-value = 2e-06
#> alternative hypothesis: true difference in means is not equal to 0
#> 95 percent confidence interval:
#> -12.4 -6.6
#> sample estimates:
#> mean of x mean of y
#> 5.5 15.0配对 t 检验:
t.test(rnorm(10), rnorm(10, mean = 1), paired = TRUE)
#>
#> Paired t-test
#>
#> data: rnorm(10) and rnorm(10, mean = 1)
#> t = -2, df = 9, p-value = 0.09
#> alternative hypothesis: true difference in means is not equal to 0
#> 95 percent confidence interval:
#> -1.419 0.134
#> sample estimates:
#> mean of the differences
#> -0.643使用公式:
df <- data.frame(
value = c(rnorm(10), rnorm(10, mean = 1)),
group = c(rep("control", 10), rep("test", 10))
)
t.test(value ~ group, data = df)
#>
#> Welch Two Sample t-test
#>
#> data: value by group
#> t = -2, df = 16, p-value = 0.03
#> alternative hypothesis: true difference in means is not equal to 0
#> 95 percent confidence interval:
#> -1.7767 -0.0945
#> sample estimates:
#> mean in group control mean in group test
#> 0.314 1.250假设方差同质:
t.test(value ~ group, data = df, var.equal = TRUE)
#>
#> Two Sample t-test
#>
#> data: value by group
#> t = -2, df = 18, p-value = 0.03
#> alternative hypothesis: true difference in means is not equal to 0
#> 95 percent confidence interval:
#> -1.768 -0.103
#> sample estimates:
#> mean in group control mean in group test
#> 0.314 1.250更多查看 ?t.test。
两总体方差检验
上面的例子假设方差同质,我们通过检验查看。
服从正态分布的两总体方差比较。
# 进行的是 F 检验
var.test(value ~ group, data = df)
#>
#> F test to compare two variances
#>
#> data: value by group
#> F = 2, num df = 9, denom df = 9, p-value = 0.3
#> alternative hypothesis: true ratio of variances is not equal to 1
#> 95 percent confidence interval:
#> 0.546 8.846
#> sample estimates:
#> ratio of variances
#> 2.2使用 Bartlett 检验比较每个组(样本)数据的方差是否一致。
bartlett.test(value ~ group, data = df)
#>
#> Bartlett test of homogeneity of variances
#>
#> data: value by group
#> Bartlett's K-squared = 1, df = 1, p-value = 0.3多个组间均值的比较
对于两组以上数据间均值的比较,使用方差分析 ANOVA。
aov(wt ~ factor(cyl), data = mtcars)
#> Call:
#> aov(formula = wt ~ factor(cyl), data = mtcars)
#>
#> Terms:
#> factor(cyl) Residuals
#> Sum of Squares 18.2 11.5
#> Deg. of Freedom 2 29
#>
#> Residual standard error: 0.63
#> Estimated effects may be unbalanced查看详细信息:
model.tables(aov(wt ~ factor(cyl), data = mtcars))
#> Tables of effects
#>
#> factor(cyl)
#> 4 6 8
#> -0.9315 -0.1001 0.782
#> rep 11.0000 7.0000 14.000通常先用 lm() 函数对数据建立线性模型,再用 anova() 函数提取方差分析的信息更方便。
md <- lm(wt ~ factor(cyl), data = mtcars)
anova(md)
#> Analysis of Variance Table
#>
#> Response: wt
#> Df Sum Sq Mean Sq F value Pr(>F)
#> factor(cyl) 2 18.2 9.09 22.9 1.1e-06 ***
#> Residuals 29 11.5 0.40
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1ANOVA 分析假设各组样本数据的方差是相等的,如果知道(或怀疑)不相等,可以使用 oneway.test() 函数。
oneway.test(wt ~ cyl, data = mtcars)
#>
#> One-way analysis of means (not assuming equal variances)
#>
#> data: wt and cyl
#> F = 20, num df = 2, denom df = 19, p-value = 2e-05这与设定了 var.equal=FALSE 的 t.test 类似(两种方法都是 Welch 提出)。
多组样本的配对 t 检验
pairwise.t.test(mtcars$wt, mtcars$cyl)
#>
#> Pairwise comparisons using t tests with pooled SD
#>
#> data: mtcars$wt and mtcars$cyl
#>
#> 4 6
#> 6 0.01 -
#> 8 6e-07 0.01
#>
#> P value adjustment method: holm可以自定义 p 值校正方法。
正态性检验
使用 Shapiro-Wilk 检验:
shapiro.test(rnorm(30))
#>
#> Shapiro-Wilk normality test
#>
#> data: rnorm(30)
#> W = 1, p-value = 0.7可以通过 QQ 图辅助查看。
qqnorm(rnorm(30))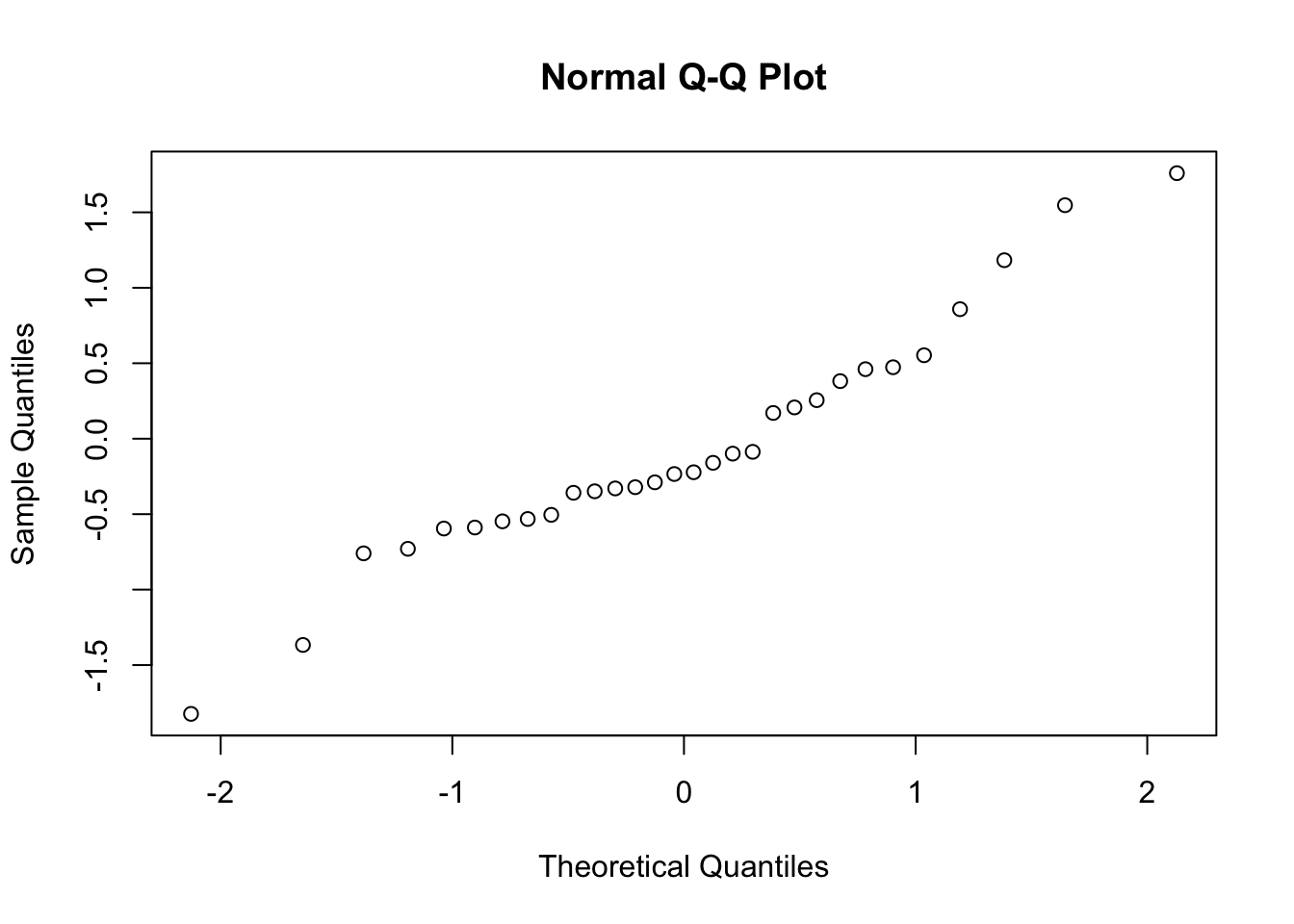
分布的对称性检验
用 Kolmogorov-Smirnov 检验查看一个向量是否来自对称的概率分布(不限于正态分布)。
ks.test(rnorm(10), pnorm)
#>
#> One-sample Kolmogorov-Smirnov test
#>
#> data: rnorm(10)
#> D = 0.2, p-value = 0.8
#> alternative hypothesis: two-sided函数第 1 个参数指定待检验的数据,第 2 个参数指定对称分布的类型,可以是数值型向量、指定概率分布函数的字符串或一个分布函数。
ks.test(rnorm(10), "pnorm")
#>
#> One-sample Kolmogorov-Smirnov test
#>
#> data: rnorm(10)
#> D = 0.4, p-value = 0.1
#> alternative hypothesis: two-sided
ks.test(rpois(10, lambda = 1), "pnorm")
#> Warning in ks.test(rpois(10, lambda = 1), "pnorm"): ties should not be present
#> for the Kolmogorov-Smirnov test
#>
#> One-sample Kolmogorov-Smirnov test
#>
#> data: rpois(10, lambda = 1)
#> D = 0.6, p-value = 5e-04
#> alternative hypothesis: two-sided检验两个向量是否服从同一分布
还是用上面的函数。
ks.test(rnorm(20), rnorm(30))
#>
#> Two-sample Kolmogorov-Smirnov test
#>
#> data: rnorm(20) and rnorm(30)
#> D = 0.2, p-value = 0.8
#> alternative hypothesis: two-sided相关性检验
使用 cor.test() 函数。
cor.test(mtcars$mpg, mtcars$wt)
#>
#> Pearson's product-moment correlation
#>
#> data: mtcars$mpg and mtcars$wt
#> t = -10, df = 30, p-value = 1e-10
#> alternative hypothesis: true correlation is not equal to 0
#> 95 percent confidence interval:
#> -0.934 -0.744
#> sample estimates:
#> cor
#> -0.868一共有 3 种方法,具体看选项 method 的说明。
cor.test(mtcars$mpg, mtcars$wt, method = "spearman", exact = F)
#>
#> Spearman's rank correlation rho
#>
#> data: mtcars$mpg and mtcars$wt
#> S = 10292, p-value = 1e-11
#> alternative hypothesis: true rho is not equal to 0
#> sample estimates:
#> rho
#> -0.886不依赖分布的检验
均值检验
Wilcoxon 检验是 t 检验的非参数版本。
默认是秩和检验。
wilcox.test(1:10, 10:20)
#> Warning in wilcox.test.default(1:10, 10:20): cannot compute exact p-value with
#> ties
#>
#> Wilcoxon rank sum test with continuity correction
#>
#> data: 1:10 and 10:20
#> W = 0.5, p-value = 1e-04
#> alternative hypothesis: true location shift is not equal to 0可以设定为符号检验。
wilcox.test(1:10, 10:19, paired = TRUE)
#> Warning in wilcox.test.default(1:10, 10:19, paired = TRUE): cannot compute exact
#> p-value with ties
#>
#> Wilcoxon signed rank test with continuity correction
#>
#> data: 1:10 and 10:19
#> V = 0, p-value = 0.002
#> alternative hypothesis: true location shift is not equal to 0多均值比较
多均值比较使 Kruskal-Wallis 秩和检验。
kruskal.test(wt ~ factor(cyl), data = mtcars)
#>
#> Kruskal-Wallis rank sum test
#>
#> data: wt by factor(cyl)
#> Kruskal-Wallis chi-squared = 23, df = 2, p-value = 1e-05方差检验
使用Fligner-Killeen(中位数)检验完成不同组别的方差比较
fligner.test(wt ~ cyl, data = mtcars)
#>
#> Fligner-Killeen test of homogeneity of variances
#>
#> data: wt by cyl
#> Fligner-Killeen:med chi-squared = 0.5, df = 2, p-value = 0.8尺度参数差异
R 有一些检验可以用来确定尺度参数的差异。分布的尺度参数确定分布函数的尺度,如 t 分布的自由度。
下面是针对两样本尺度参数差异的 Ansari-Bradley 检验。
## Hollander & Wolfe (1973, p. 86f):
## Serum iron determination using Hyland control sera
ramsay <- c(111, 107, 100, 99, 102, 106, 109, 108, 104, 99,
101, 96, 97, 102, 107, 113, 116, 113, 110, 98)
jung.parekh <- c(107, 108, 106, 98, 105, 103, 110, 105, 104,
100, 96, 108, 103, 104, 114, 114, 113, 108, 106, 99)
ansari.test(ramsay, jung.parekh)
#> Warning in ansari.test.default(ramsay, jung.parekh): cannot compute exact p-
#> value with ties
#>
#> Ansari-Bradley test
#>
#> data: ramsay and jung.parekh
#> AB = 186, p-value = 0.2
#> alternative hypothesis: true ratio of scales is not equal to 1还可以使用 Mood 两样本检验做。
mood.test(ramsay, jung.parekh)
#>
#> Mood two-sample test of scale
#>
#> data: ramsay and jung.parekh
#> Z = 1, p-value = 0.3
#> alternative hypothesis: two.sided离散数据
比例检验
使用 prop.test() 比较两组观测值发生的概率是否有差异。
heads <- rbinom(1, size = 100, prob = .5)
prop.test(heads, 100) # continuity correction TRUE by default
#>
#> 1-sample proportions test with continuity correction
#>
#> data: heads out of 100, null probability 0.5
#> X-squared = 0.01, df = 1, p-value = 0.9
#> alternative hypothesis: true p is not equal to 0.5
#> 95 percent confidence interval:
#> 0.409 0.611
#> sample estimates:
#> p
#> 0.51
prop.test(heads, 100, correct = FALSE)
#>
#> 1-sample proportions test without continuity correction
#>
#> data: heads out of 100, null probability 0.5
#> X-squared = 0.04, df = 1, p-value = 0.8
#> alternative hypothesis: true p is not equal to 0.5
#> 95 percent confidence interval:
#> 0.413 0.606
#> sample estimates:
#> p
#> 0.51可以给定概率值。
prop.test(heads, 100, p = 0.3, correct = FALSE)
#>
#> 1-sample proportions test without continuity correction
#>
#> data: heads out of 100, null probability 0.3
#> X-squared = 21, df = 1, p-value = 5e-06
#> alternative hypothesis: true p is not equal to 0.3
#> 95 percent confidence interval:
#> 0.413 0.606
#> sample estimates:
#> p
#> 0.51二项式检验
binom.test(c(682, 243), p = 3/4)
#>
#> Exact binomial test
#>
#> data: c(682, 243)
#> number of successes = 682, number of trials = 925, p-value = 0.4
#> alternative hypothesis: true probability of success is not equal to 0.75
#> 95 percent confidence interval:
#> 0.708 0.765
#> sample estimates:
#> probability of success
#> 0.737
binom.test(682, 682 + 243, p = 3/4) # The same
#>
#> Exact binomial test
#>
#> data: 682 and 682 + 243
#> number of successes = 682, number of trials = 925, p-value = 0.4
#> alternative hypothesis: true probability of success is not equal to 0.75
#> 95 percent confidence interval:
#> 0.708 0.765
#> sample estimates:
#> probability of success
#> 0.737与其他的检验函数不同,这里的 p 值表示试验成功率与假设值的最小差值。
列联表检验
用来确定两个分类变量是否相关。
对于小的列联表,试验 Fisher 精确检验获得较好的检验结果。
Fisher 检验有一个关于喝茶的故事。
## Agresti (1990, p. 61f; 2002, p. 91) Fisher's Tea Drinker
## A British woman claimed to be able to distinguish whether milk or
## tea was added to the cup first. To test, she was given 8 cups of
## tea, in four of which milk was added first. The null hypothesis
## is that there is no association between the true order of pouring
## and the woman's guess, the alternative that there is a positive
## association (that the odds ratio is greater than 1).
TeaTasting <-
matrix(c(3, 1, 1, 3),
nrow = 2,
dimnames = list(Guess = c("Milk", "Tea"),
Truth = c("Milk", "Tea")))
fisher.test(TeaTasting, alternative = "greater")
#>
#> Fisher's Exact Test for Count Data
#>
#> data: TeaTasting
#> p-value = 0.2
#> alternative hypothesis: true odds ratio is greater than 1
#> 95 percent confidence interval:
#> 0.314 Inf
#> sample estimates:
#> odds ratio
#> 6.41
## => p = 0.2429, association could not be established当列联表较大时,Fisher 计算量很大,可以使用卡方检验替代。
chisq.test(TeaTasting)
#> Warning in chisq.test(TeaTasting): Chi-squared approximation may be incorrect
#>
#> Pearson's Chi-squared test with Yates' continuity correction
#>
#> data: TeaTasting
#> X-squared = 0.5, df = 1, p-value = 0.5对于三变量的混合影响,使用 Cochran-Mantel-Haenszel 检验。
## Agresti (1990), pages 231--237, Penicillin and Rabbits
## Investigation of the effectiveness of immediately injected or 1.5
## hours delayed penicillin in protecting rabbits against a lethal
## injection with beta-hemolytic streptococci.
Rabbits <-
array(c(0, 0, 6, 5,
3, 0, 3, 6,
6, 2, 0, 4,
5, 6, 1, 0,
2, 5, 0, 0),
dim = c(2, 2, 5),
dimnames = list(
Delay = c("None", "1.5h"),
Response = c("Cured", "Died"),
Penicillin.Level = c("1/8", "1/4", "1/2", "1", "4")))
Rabbits
#> , , Penicillin.Level = 1/8
#>
#> Response
#> Delay Cured Died
#> None 0 6
#> 1.5h 0 5
#>
#> , , Penicillin.Level = 1/4
#>
#> Response
#> Delay Cured Died
#> None 3 3
#> 1.5h 0 6
#>
#> , , Penicillin.Level = 1/2
#>
#> Response
#> Delay Cured Died
#> None 6 0
#> 1.5h 2 4
#>
#> , , Penicillin.Level = 1
#>
#> Response
#> Delay Cured Died
#> None 5 1
#> 1.5h 6 0
#>
#> , , Penicillin.Level = 4
#>
#> Response
#> Delay Cured Died
#> None 2 0
#> 1.5h 5 0
## Classical Mantel-Haenszel test
mantelhaen.test(Rabbits)
#>
#> Mantel-Haenszel chi-squared test with continuity correction
#>
#> data: Rabbits
#> Mantel-Haenszel X-squared = 4, df = 1, p-value = 0.05
#> alternative hypothesis: true common odds ratio is not equal to 1
#> 95 percent confidence interval:
#> 1.03 47.73
#> sample estimates:
#> common odds ratio
#> 7用 McNemar 卡方检验检验二维列联表的对称性。
## Agresti (1990), p. 350.
## Presidential Approval Ratings.
## Approval of the President's performance in office in two surveys,
## one month apart, for a random sample of 1600 voting-age Americans.
Performance <-
matrix(c(794, 86, 150, 570),
nrow = 2,
dimnames = list("1st Survey" = c("Approve", "Disapprove"),
"2nd Survey" = c("Approve", "Disapprove")))
Performance
#> 2nd Survey
#> 1st Survey Approve Disapprove
#> Approve 794 150
#> Disapprove 86 570
mcnemar.test(Performance)
#>
#> McNemar's Chi-squared test with continuity correction
#>
#> data: Performance
#> McNemar's chi-squared = 17, df = 1, p-value = 4e-05列联表非参数检验
Friedman 秩和检验是一个非参数版本的双边 ANOVA 检验。
## Hollander & Wolfe (1973), p. 140ff.
## Comparison of three methods ("round out", "narrow angle", and
## "wide angle") for rounding first base. For each of 18 players
## and the three method, the average time of two runs from a point on
## the first base line 35ft from home plate to a point 15ft short of
## second base is recorded.
RoundingTimes <-
matrix(c(5.40, 5.50, 5.55,
5.85, 5.70, 5.75,
5.20, 5.60, 5.50,
5.55, 5.50, 5.40,
5.90, 5.85, 5.70,
5.45, 5.55, 5.60,
5.40, 5.40, 5.35,
5.45, 5.50, 5.35,
5.25, 5.15, 5.00,
5.85, 5.80, 5.70,
5.25, 5.20, 5.10,
5.65, 5.55, 5.45,
5.60, 5.35, 5.45,
5.05, 5.00, 4.95,
5.50, 5.50, 5.40,
5.45, 5.55, 5.50,
5.55, 5.55, 5.35,
5.45, 5.50, 5.55,
5.50, 5.45, 5.25,
5.65, 5.60, 5.40,
5.70, 5.65, 5.55,
6.30, 6.30, 6.25),
nrow = 22,
byrow = TRUE,
dimnames = list(1 : 22,
c("Round Out", "Narrow Angle", "Wide Angle")))
friedman.test(RoundingTimes)
#>
#> Friedman rank sum test
#>
#> data: RoundingTimes
#> Friedman chi-squared = 11, df = 2, p-value = 0.004